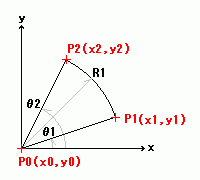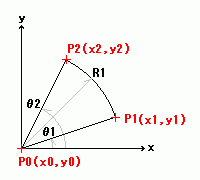続々、複線化への道(20040620)
線路の位置決めを正確に行なうには、端面の座標を求める必要があります。
直線部は簡単ですが、曲線部はちょっと面倒です。
今、下記のような曲線部について考えると、
図 曲線部の座標
P1とP2の座標は、下記のように計算できます。
x1=x0+R1×cosθ1
y1=y0+R1×sinθ1
x2=x0+R1×cosθ2
y2=y0+R1×sinθ2
なので、P1とP2の差は、下記のように計算できます。
x2−x1=R1×(cosθ2−cosθ1)
y2−y1=R1×(sinθ2−sinθ1)
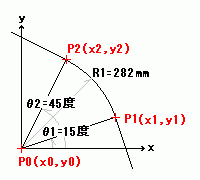
例えばR1、θ2、θ1が下記のような場合には、
図
P1とP2の差は、下記のように計算できます。
x2−x1=-73.0
y2−y1=126.4
いちいち電卓を使うのは面倒なので、計算式をプログラムにします。
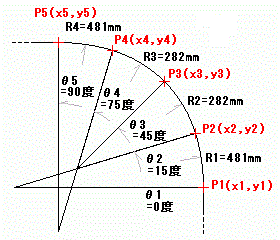
当レイアウトの曲がり部に当てはめてみると、
図
個々および全体の寸法は、下記のように計算できます。
| j |
i |
xj−xi |
yj−yi |
備考 |
| 2 |
1 |
-16.4 |
124.5 |
|
| 3 |
2 |
-73.0 |
126.4 |
|
| 4 |
3 |
-126.4 |
73.0 |
|
| 5 |
4 |
-124.5 |
16.4 |
|
| 5 |
1 |
-340.3 |
340.3 |
全体 |
表 曲線部の座標
このように計算しておくと、接続面をスムーズにつなげることができるので、脱線の危険性が減るのでした。
なにしろ脱線は、ほとんどが曲がり部(ポイントを含む)で起こると決まっていますから。