長大編成(20040801)
長大編成に心惹かれながらも、費用対効果も気になる私です。
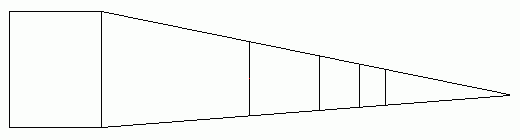
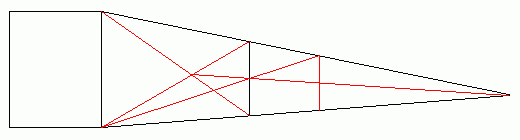
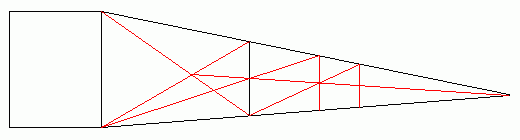
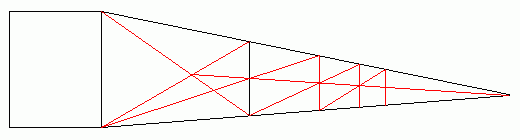
仮に無限に長い長大編成があったら、たぶんこんな風に見えるでしょう。
図 無限に長い長大編成
実物が無限の長さでも、見た目は有限の長さにしかなりません。
これは、1両目より2両目、2両目より3両目と、見た目がどんどん小さくなるからです。
すなわち、ある程度までいくと、あまり変わり映えがしない、ということです。
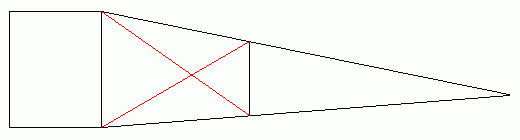
ちなみに、2両目以降の長さは下記のように求まります。
図 無限に長い長大編成の分割
あとは、繰り返しです。
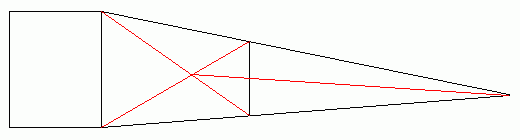
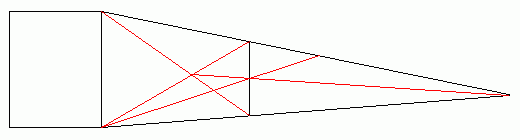
この時の、1両目と2両目の長さの比は下記のように求まります。
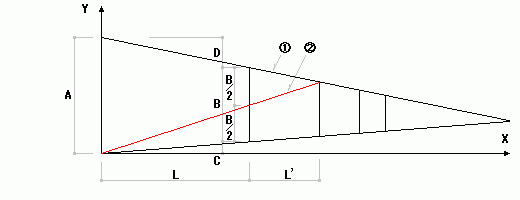
図 無限に長い長大編成の分割
直線①の式:
Y=(-D/L)X+A=(-(A-B-C)/L)X+A
直線②の式:
Y=((C+B/2)/L)X
直線①と直線②の交点のX座標(上式を等しくおく):
X=LA/(A-B/2)=L+L'
2両目の長さ:
L'=LA/(A-B/2)-L
1両目と2両目の長さの比:
L'/L=A/(A-B/2)-1
今、仮にB=0.9Aとすると(上図は0.64Aなので0.9Aはかなりユッタリした値)、
L'/L=A/(A-0.45A)-1=1/0.55-1≒0.82
| 両 |
1両目との比 |
累計 |
| 1 |
1.00 |
1.00 |
| 2 |
0.82 |
1.82 |
| 3 |
0.67 |
2.49 |
| 4 |
0.55 |
3.04 |
| 5 |
0.45 |
3.49 |
| 6 |
0.37 |
3.86 |
| 7 |
0.30 |
4.16 |
| 8 |
0.25 |
4.41 |
| 9 |
0.20 |
4.61 |
| 10 |
0.16 |
4.77 |
| 11 |
0.13 |
4.90 |
| 12 |
0.11 |
5.01 |
| 13 |
0.09 |
5.10 |
表 無限に長い長大編成の分割
11両目以降ともなると、1両目の1/10程度にしかなりません。
だからいったい何なの?というと、そう、今般、高速貨物列車を10両編成から13両編成にしたウレシサを極めて控えめに表現しているのでした。(-_-)回りくどい。
写真 高速貨物列車13両編成